Numerical Analysis and Uncertainty Quantification

Numerical Analysis and Uncertainty Quantification
Numerical Analysis and Uncertainty Quantification
Research


he partial differential equation (PDE) with random input data takes a part of the stochastic partial differential equation (SPDE) which describes the problem with uncertain inputs. Such problems occur in industries and sciences due to uncertainties of measurements, models, and so on. We can regard a SPDE as a problem depending on some parameters which take certain values in finite ranges. In this parametrization context, a SPDE is a parametrized PDE(P2DE) and one wants to simulate faster for a sequence of input data using the information on solutions at specially chosen parameters.
In the SPDE view point, we need to find out the mean of many solutions corresponding to samples. A simple method to obtain the mean of solutions is the Monte Carlo (MC) method, which requires quadruple samples to reduce the current error in half. To reduce the cost while keeping the almost same order of convergence, variance reduction techniques are suggested and studied for many variants of them, like control variate, antithetic variate, and so on.
The Multilevel Monte Carlo (MLMC) method shows a good performance in computational cost and our Projected Multilevel Monte Carlo (PMLMC) method is more faster than the MLMC method while keeping the same order of convergence. In the PMLMC method, we project the solution at fine grid into the solution space at a coarse grid. In the MLMC method, we must find a solution at the coarse grid for the same realization of randomness, which takes more computational cost. We show the PMLMC method saves the cost for the Darcy flow with a random coefficient.
In the P2DE view, we need to solve problems as fast as possible according to various combinations of parameter inputs. This is a quite natural process since many physical and engineering problems are expressed by the equations (usually PDEs) with parameters which describe physical values such as density, porosity, frequency, absorption coefficient, flow rate and so on, depending on the problem. The reduced basis method (RBM) uses the fact that a manifold of general solutions to the PDE according to the parameter is typically smooth and rather low-dimensional.
That is, the RBM saves the computational effort by the Galerkin projection of the manifold on an approximate space. We show the RBM gives us an approximate solution of the convected Helmholtz equation at least 200 times faster than the usual approximation method does.
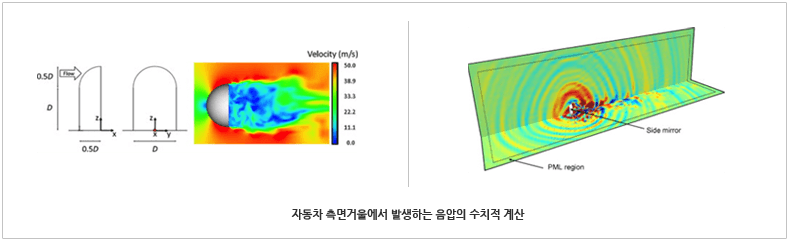
Expected effect
The accurate and reliable simulation for SPDE with uncertain inputs is of fundamental importance in a wide range of applications. Our research results can be applied to the areas of nano optics, underwater acoustics, aeroacoustics, and material sciences.
 Imbo Sim
Imbo Sim 

